Детерминанты формы временной структуры процентных ставок
При нанесении на график доходности к погашению, спот-курса и форвардных курсов против различных фоков погашения во времени вероятным сценарием может быть нормальная временная структура, имеющая восходящий уклон. Тем не менее, иногда наблюдаются другие формы, например, нисходящий уклон (как, например, в США в 1981 году) или относительно плоские или горбообразные кривые доходности. Кривая доходности в любой точке во времени представляет собой моментальный снимок различных долговых инструментов с различными сроками погашения против времени, при условии, что другие аспекты, такие как купон, кредитный риск, риск ликвидности и риск срока погашения, остаются неизменными.
Для объяснения формы кривой доходности выдвигались различные теории.
Теории ожиданий
Теории ожиданий могут принимать несколько форм: чистая теория ожиданий, теория премии за ликвидность и теория предпочтительной среды обитания. Различные формы теорий ожиданий предполагают, что форвардные курсы представляют собой рыночное согласие о будущих процентных ставках и не включают в себя никакую премию за риск с течением времени. Например, на основании чистой теории ожиданий долгосрочная ставка представляет собой геометрическое среднее портфеля краткосрочных ставок, которые, как ожидается, будут преобладать в будущем. Падающая временная структура, указывает на то, что рынок ожидает продолжения падения форвардных процентных ставок в ближайшем будущем, что имело место в прошлом вследствие падающих инфляционных ожиданий, создающих перевернутую кривую доходности, которая наблюдалась в последний рабочий день в августе 1981 г. Аналогичным образом, плоская временная структура отражает будущие краткосрочные процентные ставки, которые, как ожидается, останутся постоянными, а повышающаяся временная структура дает понять, что краткосрочные процентные ставки (форвардные курсы), как ожидается, повысятся, создавая сценарий с восходящим уклоном.
Чистая теория ожиданий подвергалась критике, поскольку она предполагает, что облигации с различными сроками погашения являются совершенными заменителями друг друга. Очевидно, что это не так. Долгосрочные облигации в большей степени подвержены более высокой цене и риску ставки реинвестирования, чем краткосрочные облигации.


Теория предпочтения ликвидности
Учитывая неуверенность в отношении будущих процентных ставок, а также большую цену и риск ставки реинвестирования, связанные с долгосрочными облигациями, инвесторы, вероятно, потребуют более высокие премии за риск, которые, как ожидается, будут равномерно увеличиваться по мере увеличения срока погашения облигации. На основании этой теории долгосрочные процентные ставки больше геометрического среднего краткосрочных ставок, которые, согласно ожиданиям, будут преобладать в будущем. Неприятие риска инвестором и неуверенность в долгосрочных облигациях, а также предпочтение большей ликвидности краткосрочных ставок увеличивают спрос на краткосрочный долг, толкая доходы вниз, а цену вверх. Точно так же предложение долгосрочного долга имеет тенденцию превышать спрос, понижая цену и увеличивая доход, а также создавая кривую доходности с восходящим уклоном. Инвесторов будет прельщать вложение капитала в рынок долгосрочных облигаций, если они будут вознаграждены за это более высокими ставками. Как говорится в теории предпочтения ликвидности, форвардная процентная ставка будет смещенным предиктором будущих краткосрочных процентных ставок.
Теория предпочтительной среды обитания
Эта теория предполагает, что временная структура включает в себя ожидание будущих процентных ставок, а также премию за риск. Тем не менее, премия за риск, как ожидается, не будет равномерно повышаться или падать по мере увеличения или уменьшения срока погашения, как утверждают сторонники теории предпочтения ликвидности. Предпочтительный горизонт инвестирования или финансирования продиктован характером активов и пассивов финансовых учреждений при принятии решений о распределении средств. Учреждения будут испытывать соблазн переместиться из своего предпочтительного горизонта, только если предлагается достаточная компенсация в форме более высокого дохода.
Например, компании страхования жизни имеют долгосрочный инвестиционный горизонт, так как их пассивы являются долгосрочными. Компании, страхующие имущество от несчастных случаев, однако, вкладывают капитал в промежуточный сегмент рынка и переместятся в долгосрочный конец рынка, только если более высокая премия за риск смягчает их неприятие процентного и ценового риска, связанного с долгосрочными облигациями.
Теория сегментации рынка
Согласно этой теории, нормативные или самоналоженные ограничения диктуют решения о распределении средств финансовых учреждений для вложения капитала в определенный сегмент рынка. Спрос и предложение в каждом сегменте рынка определяют цену, доход и форму кривой доходности. Ничто не может заставить заемщиков или кредиторов переместиться из сегмента с одним сроком погашения в другой, даже если такая возможность возникает из-за разницы доходов между любыми двумя сегментами.
Волатильность цены облигации
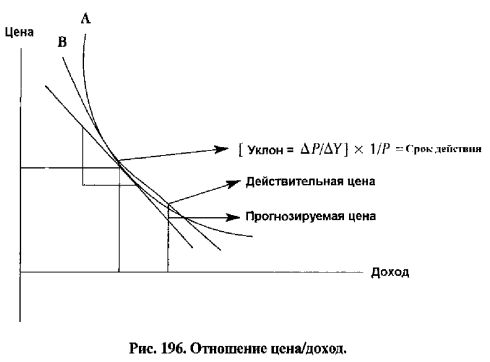
Ценовая волатильность измеряется сроком действия облигации, который равен наклону отношения цена-доход на Рис. 196, взвешенному рыночной стоимостью облигации. Срок действия – ценовая чувствительность облигации относительно изменения в доходе, и, следовательно, ее можно рассматривать как ценовую эластичность. В этом отношении некоторые облигации обладают большей ценовой эластичностью, чем другие и предлагают потенциал увеличения доходов в активном портфельном управлении.
Срок действия также может быть определен в терминах числа лет (что практикуется на Уолл-Стрит) как сумма потоков наличности, умноженная на текущую стоимость времени, в которой учитывается каждый поток наличности, взвешенный рыночной стоимостью облигации. В этом контексте срок действия измеряет размер и распределение по срокам потоков наличности в соответствии с уравнением 27:
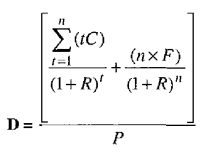
где
С – купонный процент (купонная ставка, умноженная на номинальную стоимость облигации F);
R – доходность к погашению облигации/
Р – рыночная стоимость n-летней облигации.
Выражение в скобках – это наклон отношения цена/доход ΔP/ΔY.
Срок действия трехлетней облигации в Табл. 36 рассчитан с помощью уравнения 25 и равен 2,83 года:
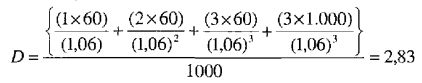
В этом уравнении получен срок действия и взвешен с помощью (1 + R), что известно как измененный срок действия (D/(l + R)). Измененный срок действия облигации равен 2,67 года. Срок действия указывает, что для каждого изменения в +/-100 базисных пунктов (1 процент) в доходе, цена облигации, как ожидается, изменится симметрично в противоположном направлении на -/+ 2,67%.
Отношение цена/доход на Рис. 196 представляет собой нелинейное выпуклое множество, поскольку процентные изменения в ценах облигаций и акций или цене любого актива, финансового или реального, несимметричны, в то время как срок действия как мера волатильности является линейным, аддитивным и симметричным.
Например, цена акции в настоящее время составляет 50 долларов. Цена поднимается до 75 долларов, принося прибыль в 50%, а с 75 долларов цена падает до 50 долларов, принося убыток в 33,33%. Процентные изменения несимметричны. Аддитивное свойство срока действия подразумевает, что срок действия портфеля – простое взвешенное среднее срока действия отдельных активов в портфеле, поскольку каждый актив взвешивается рыночной стоимостью, а не балансовой стоимостью против общей рыночной стоимости портфеля. Симметричное свойство срока действия подразумевает, что степень риска для портфеля облигаций в результате изменений в доходе на плюс или минус, скажем, 100 базисных пунктов будет одинаковой. Риск определяется в уравнении 28 как изменения рыночной стоимости портфеля активов или пассивов как ΔР = Р1 – Рt – 1, что линейно связано со сроком действия портфеля (Dp), а также с рыночной стоимостью портфеля (Р) и с изменениями в доходе (ΔY):
ΔP = – DP x P x ΔY
ΔР = -(измененный срок действия) х (рыночная стоимость портфеля) х (изменение в доходе)
Пример: Портфель облигаций в настоящее время имеет рыночную стоимость в 350 миллионов долларов с измененным сроком действия в 9,375 года. Управляющий портфелем ожидает, что ставки повысятся, поскольку появляется перспектива более высокого роста для экономики. Следовательно, управляющий портфелем рассматривает сокращение срока действия своего портфеля до семи лет, если он ожидает, что доход увеличится на 50 базисных пунктов в течение следующих трех-шести месяцев. Количество риска для этого портфеля симметрично и выражено следующим образом:
ΔР = – 9,375 ($350.000.000) (+/- 0,0050)
ΔР = +/- $16.406.250
Этот портфель, как ожидается, уменьшится или увеличится в стоимости более чем на 16,4 миллиона долларов при увеличении или уменьшении дохода на 50 базисных пунктов, поскольку доход и цена обратно пропорционально связаны. Когда изменения дохода являются небольшими, срок действия обеспечивает оценку риска, близкую к фактическим изменениям в рыночной стоимости портфеля; тем не менее, когда изменения дохода являются большими, срок действия недооценивает фактические изменения в цене облигации при изменении цены облигации в любом направлении.
Долларовую стоимость одного (Dollar value of one – DVO1) базисного пункта можно оценить, используя уравнение 28 для облигации или портфеля кредитов. Например, DVO1 для этого портфеля равна:
ΔР = – 9,375 ($350 000 000) (+/- 0,0001) = +/- $328 125
Ожидается, что стоимость портфеля изменится на +/-328 125 долларов при каждом изменении в один базисный пункт в доходе. DVO1 передает полезную информацию управляющему портфелем, и некоторые вебсайты, такие как Bloomberg и Reuters, сообщают эти статистические данные своим клиентам.
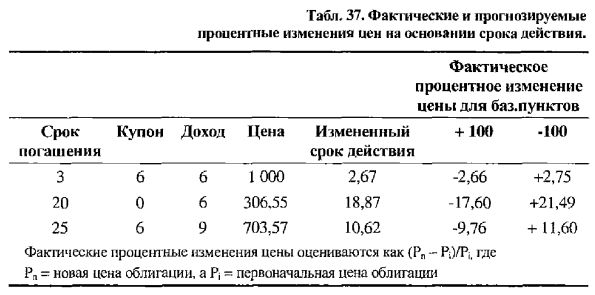
Рассмотрим три облигации в Табл. 37, прогнозируемые процентные изменения цен, основанные на сроке действия, и фактические процентные изменения цен при изменении в доходе на плюс или минус 100 базисных пунктов.
20-летняя облигация с нулевым купоном имеет самую высокую ценовую волатильность, что отражено в измененном сроке действия в 18,87 года. Фактическое процентное изменение цены для этой облигации составляет -17,60 и +21,49 процента соответственно при изменении в доходе на +/-100 базисных пунктов, как показано в Табл. 37. Прогноз, основанный на сроке действия, предсказывает, что цена предположительно изменится на +/-18,57 процента на каждое 1-процентное изменение в доходе. Недостаточно одного срока действия, чтобы уловить процентное изменение цены облигации вследствие выпуклости этой облигации.
Точно так же 20-летняя облигация в Табл. 37 имеет большую выпуклость, чем две другие облигации, что отражено в фактических изменениях цены при изменении дохода на +/-100 базисных пунктов при сравнении с двумя другими облигациями. Выпуклость захватывает кривизну отношения цена-доход, поскольку облигация А на Рис. 196 обладает более высокой выпуклостью (положительной) по сравнению с облигацией В. Цена положительно выпуклой облигации, как ожидается, больше увеличится при уменьшении в доходе, в то время как в случае увеличения дохода цена упадет меньше, чем цена облигации с меньшей выпуклостью или без выпуклости.
Например, для 3- и 25-летних купонных облигаций фактические процентные изменения цен и прогноз процентных изменений цен, основанный на их соответствующем сроке действия, приблизительно близки, как показано в Табл. 37. Например, цена 25-летней купонной облигации, как ожидается, изменится на +/-10,62 процента, что отражено в ее сроке действия. Тем не менее, фактические процентные изменения цен этой облигации составляют соответственно -9,76 и +11,6 процента при изменении в доходе на +/-100 базисных пунктов (Табл. 37).
|