9.3.3. О законах (теоремах) арксинуса
"Законы арксинуса" (известные также как первая и вторая теоремы), в частности, показывают, что в случайных процессах тренды возникают почти неизбежно. Мы не будем утомлять читателя математикой строгих выкладок. Но если кому-то хочется узнать об этой интересной особенности жизни случайных чисел, с тем чтобы применить ее на практике, то ниже будет дана общая формулировка первого закона, кратко изложенного в прикладной форме.
Обратимся опять к монете. Но не как к дорогому сердцу всякого трейдера денежному знаку, а в качестве генератора случайных чисел. Вновь займемся бросками на удачу и результат каждого испытания будем обозначать точкой в двухмерном пространстве:
по вертикали. Шаг вверх, если выпадает какая-то заранее обозначенная сторона (прибыль); если другая – шаг вниз (убыток);
по горизонтали. Каждый номер броска – это один шаг вправо (очередное вхождение в рынок).
В результате множества бросков получим набор точек, соединив которые, увидим некоторую линию, берущую начало из координаты (0, 0), а далее уходящую в неизвестность. Такой путь в теории вероятности называют кривой "случайного блуждания". Очевидно, что она весьма близко отражает игровую ситуацию "трейдер против рынка". Игрок тоже "блуждает" по этому минному полю, то выигрывая (допустим, верхняя половина пространства), то теряя (нижняя). Поэтому задачи, теоретически решаемые в связи с этой моделью, могут иметь для нас известное практическое значение.
Вопрос формулируется просто: если рынок считать явлением случайным и поэтому решение об открытии позиции принимать на основе серии последовательных бросков монеты "угадал – не угадал", то какова вероятность оказаться в выигрыше (в данном случае – в верхней части пространства блуждания) по суммарным результатам какого-то определенного числа испытаний?
Здравый смысл подсказывает, что раз процесс случайный, то и распределение точек по обе стороны разделительной полосы должно быть приблизительно равномерным. Но эта подсказка никуда не годится. Потому что одно из самых неожиданных свойств чистой случайности заключается в том, что равномерное распределение после каждой отдельной серии испытаний встречается крайне редко.
Собственно говоря, в этой истине и состоит первый закон арксинуса. Он разрушает наши интуитивные представления о том, что при бросках "идеальной" монеты выигрыш примерно должен быть равен проигрышу. И дело в том, что это не просто неверно, а совершенно неверно. Иными словами, подсказка здравого смысла и реальная действительность стоят друг от друга, как мы увидим, на весьма неблизком расстоянии.


Если говорить более конкретно, то согласно первому закону арксинуса при фиксированном t (0P = (2/3,14)x arcsin(t)1/2.
Графически функция Р = f(t) представляет собой кривую такого вида (см. рис. 14):
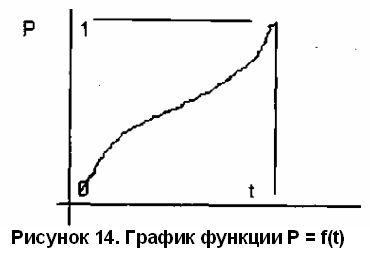
Хотя формула выведена для условия бесконечного числа бросков, но приличное ее приближение фактически обеспечивается начиная уже с 20 испытаний.
Из этого закона следуют два важных вывода.
Во-первых: вероятность для трейдера провести большую часть времени на выигрышной стороне гораздо ближе к 0 или 1, чем к интуитивно ожидаемому значению 1:2.
Во-вторых: чем больше число испытаний, тем более очевидным будет волновой характер случайного блуждания, при котором все точки будут группироваться примерно по синусоиде (не отсюда ли "правило перемен" Эллиотта?).
Проиллюстрируем сказанное примером, который приведен у Феллера (см. [34], с. 96):
Опыт: монету подбрасывают каждую секунду на протяжении целого года.
Интересующее событие: вероятность (Р) того, что менее удачливый игрок будет находиться в выигрыше не более чем Т дней в году.
Результаты:
T=154, 126, 100, 75, 50, 35, 20, 9, 2;
Р = 0,9, 0,8, 0,7, 0,6, 0,5, 0,4, 0,3, 0,2, 0,1.
Это значит, в частности, что с вероятностью 0,9 более удачливый игрок будет в выигрыше 211 дней в году, т.е. почти 60% времени. Неплохо!
Расчеты для 10 000 испытаний показывают: вероятность того, что одна играющая сторона находится в выигрыше более 9930 раз, а другая – менее 70, больше 0,1. Интуитивно такой исход кажется маловероятным. В действительности получается, что один эксперимент из 10 может привести к такому совершенно непропорциональному соотношению, как 9930:70 в пользу одного из игроков. Иными словами, из 10 трейдеров, использующих метод случайных чисел, один будет исключительно удачлив, с вероятностью 90%. (Вспомним в этой связи, что ранее мы приводили оценки отсева обучающихся: из каждых 100 на рынке остаются 10. Совпадение поразительное, не правда ли?)
Таким образом, важнейшее практическое следствие закона в том, что в деле "трейдер против рынка" самый невероятный исход – это ничья. И куда более вероятен будет вариант, когда одна из сторон будет "более удачлива", а другая – "менее удачлива".
Несколько слов о втором законе арксинуса.
Введем понятие "максимум" применительно к графику случайного блуждания: это вершина, пика которого точка блуждания достигает в верхней (выигрышной) половине графика. Смысл понятия в том, что в этом месте наш игрок достигает наилучших результатов за какой-то прошедший период времени бросания монеты.
Второй закон арксинуса устанавливает наиболее вероятные места расположения максимумов по ходу игры. Было доказано, в частности, что существует сильная тенденция к расположению максимумов в начале пути блуждания. Иначе говоря, более вероятно оказаться в выигрыше в начале испытаний, чем в середине. Не потому ли родилось выражение "новичкам везет"?
И еще один практический вопрос, ответ на который дают законы арксинуса. Допустим, что игрок решает прекратить игру в момент, когда он имеет любой положительный результат. Каково время ожидания такого исхода? Расчеты показывают, что время возникновения чистого выигрыша "когда-нибудь обязательно наступит". Это звучит так же оптимистично, как и обещание светлого будущего, которого можно и не дождаться.
Наконец, замечания о связи теорем арксинуса и закона больших чисел.
Как отмечалось выше, первый закон арксинуса противоречит здравому смыслу. Но это не беда. Гораздо хуже – противоречие незыблемому закону больших чисел. Вспомним, что последний гласит: с возрастанием числа испытаний успех должен неизбежно уравниваться неудачей.
На самом деле противоречия здесь нет. Закон больших чисел потому так и называется, что он справедлив только для возрастающего до бесконечности числа серий испытаний. Именно тогда доля выигрыша стремится к 1:2. Но этот закон ничего не говорит о том, что будет происходить в каждой отдельной серии. А вот первый закон арксинуса как раз именно об этом: ничья на конкретно ограниченном отрезке бесконечного пути испытаний маловероятна.
К сожалению, никто не в состоянии заранее и точно подсказать трейдеру, начавшему игру против рынка, кто из них на деле окажется удачливее.
Впрочем, есть еще один способ оценить свое будущее, опираясь на первый закон арксинуса.
Дело в том, что значение законов арксинуса выходит за "монетные" рамки и имеет даже философское звучание. Отмеченные закономерности не только являются особенностью игры с бросанием монет, но и характерны для более широкого класса случайных величин. Мы живем в мире, полном случайностей, каждый из нас не раз убеждался, что и в жизни есть более и менее удачливые люди: одни – явные "везунчики", у других ничто не ладится, а третьих словно на волнах качает: то холодно от неудач, то жарко от счастья. Не правда ли, в этом невольно видится проявление первого закона арксинуса? Поэтому каждый трейдер, решивший испытать действие данного закона на себе, должен проанализировать свой жизненный путь, и, если он увенчан не шипами, а розами, есть весомые шансы, что изначально присущая удачливость может найти свое продолжение и в трейдинге. С другой стороны, человеку, которому в жизни "вечно не везет", возможно, родился не с той стороны синусоиды, и ему лучше воздержаться от испытания своей невезучести на валютном рынке. Однако здесь ничего заранее предопределенного нет, есть только вероятностная оценка. Не исключено, что даже самый неудачливый в жизни человек вдруг получит лакомый кусок своей синусоиды в трейдинге. В конце концов каждый живущий на Земле человек уже априори является "везунком": ведь ему дарован шанс появиться на свет, опередив многих менее удачливых претендентов на жизнь.
Но оставим "философию арксинуса" и вернемся к теории вероятности с точки зрения практического вопроса: "Что делать?"
Если принять факт постоянной смены подъемов и падений рынка как самое что ни на есть присущее случайным процессам свойство, то хорошо бы научиться оценивать вероятную продолжительность конкретных ценовых движений рынка. Посмотрим, как это можно было бы осуществить.
|