Волатильность
Вышеуказанная доходность не является нормально распределенной. Она таковой не является, потому что мы предположили, что генератор доходности периодов – логарифмически нормальный процесс. Проценты не являются логарифмами. Мы можем преобразовать ряд в левой таблице в логарифмический ряд, взяв натуральный логарифм каждого (1 + % доходности периода). Это дает нам ряд в правой таблице. Для ясности необходимо отметить, что эти значения – логарифмы от «единица плюс доходность в процентах», то есть они являются «связующими» значениями для каждого периода актива. Поскольку они являются логарифмами, они аддитивны, кроме того, поскольку они являются логарифмами (и мы принимаем логарифмически нормальное распределение), они нормально распределены. Вот этот ряд мы и должны измерить на волатильность, а не ряд доходности в процентах.
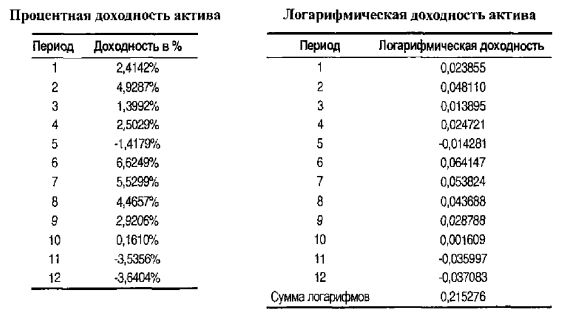
Чтобы подтвердить аддитивный характер такой логарифмической доходности, читатель должен взять показательную функцию (или «антилогарифм») суммы (0,215276), и он найдет, что она равна 1,2402. Уберите 1, и перед вами ежегодная процентная доходность в 24,02% – иллюстрация того факта, что методологии доходности (логарифмической и процентной) являются (совершенно) одинаковыми.


Вычисление традиционной волатильности (стандартного отклонения) для ряда доходности заключается в том, чтобы взять корень из [(суммы квадратов отличий процентной доходности от среднего)(n – 1)], или в алгебраическом выражении:
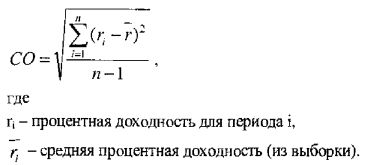
Такое вычисление дает волатильность на горизонте частоты периода, так что в данном случае это ежемесячная волатильность. Если мы хотим пересчитать ее на год, мы используем Центральную предельную теорему, которая говорит нам, что если доходности периодов статистически независимы друг от друга, волатильность на любом горизонте является квадратным корнем из [(желаемый горизонт)/(горизонт периода)], измеряемым в последовательных единицах времени (дни, месяцы, годы). Например, пересчитывание ежемесячной волатильности на год означало бы умножение результата вышеупомянутой формулы на √(12/1) = 3,464.
Кстати, скажем несколько слов о Центральной предельной теореме. Это статистический закон, который широко (часто бессознательно) используется в анализе инвестиционного менеджмента. В сущности, она постулирует, что если берется ряд наблюдений независимой случайной переменной, то стандартное отклонение получаемого в результате выборочного среднего представляет собой стандартное отклонение лежащей в основе совокупности, разделенной на квадратный корень из числа наблюдений. Кроме того, даже если лежащее в основе распределение ненормально (даже очень ненормально), распределение выборочного среднего стремится к нормальности по мере роста числа наблюдений в выборке. Для самых независимых переменных объем выборки, равный 10, становится довольно нормальным.
Центральная предельная теорема – основание для всей конверсии стандартных отклонений на различных частотах данных. Логика такова (заметьте, что доходность – это натуральный логарифм (1 + процентная ежемесячная доходность)).
Предположим, что мы измеряем доходность ежемесячно. Чтобы вычислить годовой доход, мы суммируем ежемесячные доходности. Это представляет собой сумму (то есть 12 х среднее) выборки из 12 наблюдений. Стандартное отклонение средней ежемесячной доходности в этой выборке согласно Центральной предельной теореме будет равно (Ежемесячное стандартное отклонение)/(Кв. корень из 12). Но нас интересует ежегодная сумма, а не ежемесячное среднее. Она в 12 раз больше ежемесячного среднего, так что нам нужно умножить приведенное выше выражение на 12:
Ежегодное стандартное отклонение = (Ежемесячное стандартное отклонение)/(кв. корень из 12) х 12 = (Ежемесячное стандартное отклонение) х (кв. корень из 12)
Следовательно, частный случай пересчитывания на год волатильностей требует, чтобы мы умножали на корень из числа наблюдений в году.
Хотя Центральная предельная теорема очень эффективна при преобразовании любого распределения в нормальное, она работает только в том случае, если переменные в выборке независимы. Следовательно, она остается сильной теоретической возможностью того, что валютный рынок и другие рынки не являются нормальными на одногодичном горизонте, если составляющие переменные (ежедневная, еженедельная, ежемесячная доходность) являются некоторым образом сериально коррелированными.
Так, с помощью этой информации и калькулятора мы можем подсчитать, что ежемесячная волатильность вышеупомянутого ряда составляет 3,40%, а пересчитанная на год волатильность – 11,79% (=3,40% х 3,464). Однако такой результат будет при взятии таких данных, в отношении которых мы знаем, что они ненормальны (процентная доходность). Ненормальные данные, вероятно, дадут нам непредсказуемые и неожиданные результаты и не поддадутся ряду статистических испытаний, что делает нормальное распределение таким полезным, и, как ни удивительно, Центральная предельная теорема не собирается помогать нам «делать распределение нормальным».
|