9.3.1. Случаен ли рынок
Известно, что рынок уж слишком часто позволяет себе довольно неуважительное поведение по отношению к прогнозам даже самых маститых авторитетов. И все же интересно, можно ли проанализировать рынок доступными научными методами на предмет его случайности?
Сформулируем нашу позицию еще раз следующим образом. Появление факторов, которые воздействуют на цены, вызывая их движение в какую-то сторону, несомненно носит случайный характер. Никто (кроме астрологов) не может заранее знать и рассчитать, что и как повлияет на рынок в каждый последующий момент. Однако отдельные случайные движения в конечном итоге складываются в такую конфигурацию, где можно углядеть определенные закономерности. Например, если сложилось так, что цены все же куда-то серьезно двинулись, то происходит это уже несколько организованнее, т.е. с моментами закономерной упорядоченности. Тогда поведение рынка становится и более предсказуемым, хотя такие периоды тоже могут появляться случайно. И этому можно найти подтверждение с помощью вероятностных методов анализа.
В качестве предварительного замечания подчеркнем, что, строго говоря, любой анализ валютного рынка, в том числе фундаментальный, технический, компьютерный или какой-то иной, – это анализ в известной мере и вероятностный. Одним из практических следствий признания такого положения является обязательность постановки ордера Stop-loss при открытии торговой позиции, вне зависимости от того, насколько уверен в себе трейдер. Потому что ни один из упомянутых аналитических подходов не дает стопроцентной гарантии надежности получаемых оценок.
Отличие вероятностного подхода как самостоятельной системы анализа не только в том, что здесь этот акцент приобретает форму приоритета, но и в попытке дать на основе методов теории вероятности два вида количественных расчетов.
Во-первых, – оценку того, насколько рынок действительно случаен как явление вообще и в данный конкретный период времени своего развития в частности.
Во-вторых, на основе вероятностного подхода можно выносить статистически обоснованное суждение о надежности заключений прогностического характера.
Надо сказать, что работ на эту тему пока не так много (см. например, Tadion), хотя проблема заслуживает гораздо большего внимания.
Проверить рынок на случайность можно разными способами, причем более научными, чем метание дротиков в газету. Наглядный пример применения классических вероятностных методов анализа к валютному рынку приведен у Тадиона, который на основе случайных чисел строит график, внешне напоминающий движение цен (см. [21]).


Каждый читатель может самостоятельно проделать процедуру, описанную в любом учебнике по теории вероятности: из таблицы случайных чисел нужно сделать выборку, скажем, объемом в 500,1000,10000 и т.д. При этом пусть каждое из случайных чисел может изменяться в каком-то заданном интервале (от 0 до 99 или от 0 до 1). Проведя такую кропотливую работу, получим осциллятор с колебаниями от О до 99 около оси среднего, которое примем равным 50. Значения тех случайных чисел, что выше 50, обозначим как положительные, а остальные (т.е. ниже этого среднего) – как отрицательные. На графике отложим: по горизонтали – номер числа, а по вертикали – его соответствующее положительное или отрицательное значение. При этом будем отсчитывать каждое последующее число от значения предыдущего.
Например, ряду случайных чисел 31, 72, 44, 99, 2 соответствуют значения:
–19 (т.е. 31 – 50); +22 (т.е. 72 – 50); –6 (44 – 50); +49 (99 – 50), –48 (2 – 50).
На графике этот ряд преобразуется так (см. рис. 12):
–19; +3 (т.е. –19 + 22= 3); –3 (+3 – 6 = –3); +46 (–3 + 49 = +46); –2 (46 – 48 = –2).
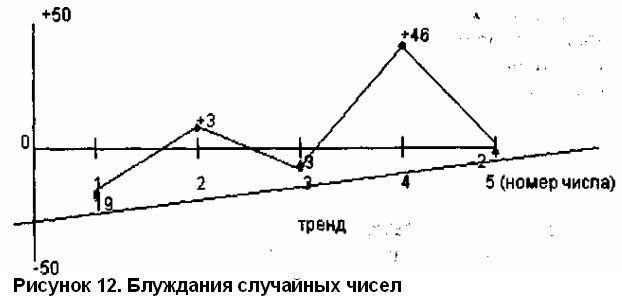
Даже по этой небольшой выборке всего из пяти элементов мы видим наметившийся "случайный тренд". Если провести построение графика для всех 500 чисел случайной выборки, то картинка покажет поразительно близкую аналогию реальному рынку. Там можно будет найти все: и линии, напоминающие поддержку и сопротивление, регулярно случающиеся подъемы и спады. В общем, все как и положено для случайных процессов (см. рис. 13).
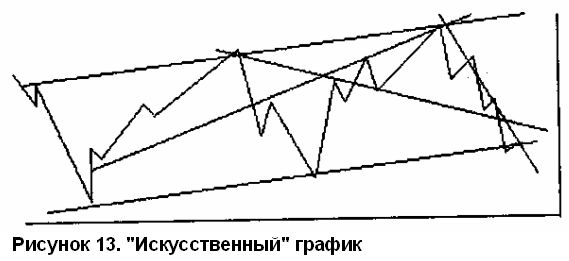
Такие графики справедливо называют "искусственными" (artificial charts), а недоброжелатели пытаются "обидеть" их, обозначив не более как "предметами любопытства" (curiosities).
Однако их значение выходит далеко за рамки праздного заглядывания в тайны Природы. Как бы ни "оскорбляли" эти графики, но они убедительно показывают следующее: по чисто внешним признакам "рынок случайных чисел" принципиально не отличается от поля боя, где валютные дилеры ведут реальную борьбу за свои доходы, воображая при этом, что знают какие-то тайны движения цен.
Правда, с научной точки зрения похожесть не означает тождественность. И рынок дает поразительные примеры того, на что он может быть похож. Так, известен случай, когда график движения биржевых цен на довольно продолжительном отрезке времени "один в один" повторял, причем с нужным запаздыванием, кривую побед и поражений какой-то американской бейсбольной команды. Иными словами, если бы в тот период кто-то отважился делать биржевые ставки исходя не из конъюнктуры рынка, а по результатам бейсбольных игр, он победил бы этот рынок за явным преимуществом.
Согласно другим недавним наблюдениям, движение цен на биржевом рынке коррелирует с длиной модного дамского платья: чем выше подол, тем быстрее растут котировки.
Ну и что? А то, что случайные процессы могут порой принимать какие угодно внешние формы, в том числе и такие, которые напоминают закономерности, выведенные экспертами и теоретиками или придуманные "финансовыми астрологами".
Можно подойти к оценке "случайности" реального рынка и с другой стороны, т.е. отталкиваясь уже непосредственно от действительного поведения самих цен. В этих целях используют статистическую теорию серий. Сериями принято называть повтор элементов одинакового типа в смешанной последовательности различных элементов. Например, последовательность АААВВАВВВВ начинается А-серией длины 3, за которой следует В-серия длины 2 и т.д. Применение теории серий в статистике связано с проверкой результатов наблюдений на случайность. Для нас это как нельзя кстати.
Проделаем следующую процедуру: если текущее значение рынка больше предыдущего, обозначим его каким-то одним символом, а если меньше, то другим, например, соответственно 1 и 0 (отсутствие изменений засчитывать не будем). В результате для проверки на случайность получится последовательность серий из единиц и нулей.
Если изложить методику упрощенно, то "рыночная" конфигурация из серий нулей и единиц статистически сравнивается со "случайным рядом", который получается при броске монеты (ноль – орел, единица – решка) или от генератора случайных чисел в интервале от 0 до 1 (нижняя половина интервала принимается за 0, верхняя – за 1). Иначе говоря, конкретные "рыночные" серии рассматриваются с точки зрения того, какова вероятность их возникновения при условии полной случайности.
Упомянутый выше автор Tadion протестировал "на случайность" рынок "большой пятерки" валют за период с 1979 по 1993 год и пришел к заключению, что не все там так уж случайно, как может показаться. Однако прежде чем сказать об этом подробнее в следующем подразделе, мы ненадолго отвлечемся, чтобы дать некоторые понятия теории вероятности, связанные с бросками монеты. Это важно для дальнейшего понимания излагаемого материала и самостоятельной аналитической работы трейдера.
О некоторых понятиях теории вероятности
Прежде всего определим содержание используемой терминологии.
Событие (или исход) – это результат мысленных или реальных опытов и экспериментов. (Отметим отличие между опытом и экспериментом: в первом случае интересно посмотреть, что вообще получится, тогда как во втором – проверяется справедливость той или иной предварительно выдвинутой гипотезы).
Подбрасывание монеты (в виде опыта или эксперимента) может приводить к самым разным результатам. Любой из них – это несомненно событие.
Разумеется, они бывают разные. В теории вероятности их подразделяют на два вида: составные, которые можно разложить на части, и элементарные, т.е. никак дальше не разложимые. Например, событие "выпадение решки при первых двух бросках" разлагается на два элементарных: "решка при первом броске" и "решка при втором броске", каждое из которых далее уже разложить невозможно.
Применительно к какому-то определенному опыту (эксперименту) говорят о совокупности элементарных событий, представляющих собой все мыслимые и неразложимые исходы испытаний. Эти исходы называют пространством, или полем элементарных событий для данного опыта.
Если, скажем, опыт включает только один бросок монеты, то это поле состоит всего из двух элементов: "орел", "решка".
Для опыта, состоящего из двух последовательных бросков монеты, пространство элементарных событий будет иным. Оно содержит уже четыре элемента: "орел–орел", "орел– решка", "решка–орел", "решка–решка".
Что касается составных событий, то примером может быть: "выпадает или орел, или решка". (Подчеркнем наличие здесь важного упрощающего допущения: монета "идеализируется" в том смысле, что, во-первых, исключается такое крайне маловероятное элементарное событие, как выпадение ее "на ребро", и, во-вторых, игнорируются какие-либо физические перекосы, в результате которых монета становится "неравномерной".)
При одновременном и единоразовом броске двух монет поле неразложимых событий будет состоять из тех же элементов, что и в предыдущем случае, но сложные события могут формулироваться несколько иначе, поскольку бросок только один, а монеты две (там была одна монета и два броска): "обе монеты падают одинаковыми сторонами", "одна монета падает так, а другая иначе" и др.
Таким образом, с монетами возможны различные типы опытов-экспериментов в зависимости от количества одновременно используемых монет и числа проводимых с ними испытаний. Но важное отличие между ними в том, что при единоразовом испытании с несколькими монетами одновременно составные события не включают в себя порядка выпадения "орлов" и "решек", а только их разные комбинации, в то время как при последовательных бросках порядок выпадения может иметь свое немаловажное значение.
Первое: если все элементарные события равновероятны, то вероятность составного будет определяться долей тех элементарных, что входят в составное, в полном. их пространстве. Или иначе: вероятность составного события есть сумма вероятностей его элементарных составляющих.
Второе: для любых двух событий X и Y, вероятность которых соответственно В(Х) и B(Y), вероятность того, что случится и то и другое B(X,Y), определяется по формуле: В(Х) х B(Y). Для несовместимых событий B(X,Y) = 0.
Третье: для любых двух событий X и Y, вероятность которых соответственно В(Х) и B(Y), а вероятность их совместного наступления равна B(X,Y), вероятность того, что имеет место либо одно, либо другое, либо оба эти события вместе, вычисляется по формуле: В(Х) + B(Y) – B(X,Y). Для случая несовместимых событий X и Y формула упрощается до В(Х) + B(Y).
При каждом отдельном броске "идеальной" монеты (это та, что и на ребро не падает, и перекосов не имеет) вероятность выпадения любой из двух сторон равна 1:2.
Теперь можно приступить к вычислениям применительно к некоторым из составных событий, упоминавшихся выше.
Опыт: один бросок монеты.
Поле элементарных событий: "орел", "решка".
Интересующее составное событие: "выпадает или орел, или решка", т.е. здесь включено все поле элементарных событий.
Результат (вероятность составного события) по третьему правилу:
0,5 + 0,5 = 1.
Это, мягко говоря, вовсе не противоречит здравому смыслу: что-нибудь да обязательно выпадет. Можно было бы и не вычислять.
Но пусть читатель потерпит, поскольку в этом разделе у него еще будет возможность убедиться, как здравый смысл способен подводить, а теория вероятности, напротив, – наставлять на путь истинный.
Пойдем дальше.
Опыт: два последовательных броска монеты.
Поле: "о, о"; "о, р"; "р, о"; "р, р"; по второму правилу все эти события равновероятны, т.е. каждое характеризуется вероятностью 1:2 х 1:2 = 1:4.
Интересующее событие №1: "выпадают два орла", т.е. включает в себя только одно из элементарных событий – "о, о".
Результат оценки по первому правилу: 1:4.
Интересующее событие №2: "при втором броске выпадает решка"; сюда попадают два элементарных события – "о, р" и "р, р".
Результат по первому правилу: 1:4+1:4=1:2.
Интересующее событие №3: "выпадает хотя бы одна решка" (интересно, что здесь читателю подсказывает интуиция?); из поля элементарных событий подходят три – "о, р"; "р, о"; "p, p".
Результат по первому правилу: 1:4 + 1:4 + 1:4 = 0,75.
Опыт: три последовательных броска монеты.
Поле (восемь элементов): "о, о, о"; "о, о, р"; "о,р,о"; "р, о, о"; "о, р, р"; "р, о, р"; "р, р, о"; "р, р, р"; по второму правилу вероятность каждого 1:2 х 1:2 х 1:2 = 1:8.
Интересующее событие: "выпадает три орла подряд"; здесь включено только одно элементарное событие – "о, о, о".
Результат по первому правилу: 1:8.
Кстати говоря, из первого правила вытекает, что при N бросках монеты вероятность выпадения "орла" N раз будет равна 1:2, возведенным в степень N. Это знание пригодится нам при последующем рассмотрении вопросов, связанных с тестированием рынка на случайность исходя из очевидной посылки о том, что чем чаще повторяются маловероятные события, тем меньше в этом случайности.
Опыт совсем иного типа: бросаем монету до тех пор, пока два раза подряд не выпадет одна и та же сторона.
Поле содержит бесконечное число элементов (т.е. теоретически опыт может не закончиться никогда).
Интересующее событие: "опыт кончится до шестого бросания"; из всего множества элементарных событий подходят следующие – "о, о"; "р, р"; "о, р, р"; "р, о, о"; "р, о, р, р"; "о, р, о, о"; "о, р, о, р, р"; "р, о, р, о, о". Здесь уже элементарные события, входящие в составное, не равновероятны и просчитываются по второму правилу: 1:4; 1:4; 1:8; 1:8; 1:16;1:16; 1:32; 1:32.
Результат по первому или третьему правилу: 2 х (1:4 + 1:8+1:16+ 1:32) = 15:16 = 0,94.
Если видоизменить тот же опыт до "бросаем до тех пор, пока дважды подряд не выпадет орел", то результат по аналогичному интересующему событию: 0,47.
Итак, последовательность решения вероятностных задач с "идеальной" монетой заключается в следующем.
1. Определяем точное содержание опыта-эксперимента с точки зрения числа монет и бросков.
2. Заполняем пространство элементарных событий всеми мыслимыми вариантами.
3. Формулируем интересующее нас составное событие с точки зрения того, какие из элементарных оно включает.
4. Делаем соответствующие вычисления на основе трех правил.
Какой для нас смысл в этих, казалось бы, далеких от дилинга монетных абстракциях? Простой: каждая ставка трейдера на основе, например, одного лишь интуитивного ощущения либо какого-то индикатора сравнима с броском монеты. Сколько вхождений в рынок, столько и бросков одной и той же монеты.
А использование сразу нескольких технических индикаторов похоже на одновременный бросок всех монет в количестве, соответствующем числу индикаторов. Сколько раз так трейдер открывает позиции, столько же и одновременных бросков комплекта монет.
О проверке рынка на "случайность"
Как мы видели, при бросках "идеальной" монеты вероятность выпадения подряд какой-то одной стороны тем меньше, чем больше "заказывается" таких выпадений. Это означает, что в "случайном" рынке выпадение одних и тех же сторон в количестве 2, 3, 4, 5, 6 и т.д. должно происходить все реже и реже по мере возрастания их числа по приведенной ранее формуле (1/2 в степени n, где n – число одинаковых выпадений).
А что мы наблюдаем с этой точки зрения на реальных графиках? Так оно и есть. Если взять графики всех упомянутых валют и перевести их в серии единиц и нулей, то они окажутся достаточно перемешанными, чтобы говорить о каких-то значимых отклонениях от случайных распределений. Однако картина неожиданно меняется, если отфильтровать "шумы и помехи", вносимые мелкими флуктуациями, случайность которых признавал даже Эллиотт. В качестве такого отсекающего фильтра используются движущиеся средние. Действительно они приводят ряд мелких колебаний к некоторой одной усредненной величине, игнорируя тем самым имеющиеся случайные различия.
Очевидно: чем длиннее интервал усреднения, тем больше случайностей будет исключено и возможно проявление того, что за этим стоит. В результате выявилось, что по мере увеличения интервала усреднения от 1 до 10 идет явное уменьшение признаков "случайности", и скрытые в более мелких флуктуациях тренды как бы обнажаются. Впрочем, если постараться, их можно обнаружить и визуально. Интересно то, что в "очищенном" виде нули или единицы регулярно повторяются с точки зрения случайных процессов многие десятки раз подряд.
Эти результаты подтверждают сформулированное выше положение, что если рынок вошел в тренд, он там будет пребывать некоторое время. К большому сожалению, воспользоваться данным свойством не так просто, поскольку совершенно случайным остается проявление двух практически важных моментов:
а) когда, через сколько шагов, на каком этапе возникнет тренд;
б) какой он будет продолжительности.
Как видно, мы вновь уперлись в тот же фундаментальный и нерешенный вопрос о том, каким образом трейдеру заблаговременно определить, находится ли он в данный момент еще в тренде, или последний уже завершился. Единственный выход – это делать какие-то предположения и выдвигать рабочие гипотезы, которые должны быть чем-то обоснованы. С точки зрения теории вероятности такое обоснование следует искать в статистических данных.
|